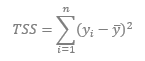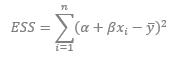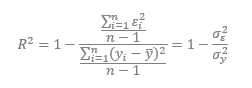R-Squared
The coefficient of determination for a regression equation is commonly referred to as R-squared, or just R2. R2 is often described as the goodness of fit, and measures how well the regressors or independent variables explain the regressand or dependent variables. R2 can range from 0 to 100%. If R2 is equal to 100%, then the regression model completely explains all the variability in the dependent variable. If R2 is equal to zero, then the regression does not explain any of the variability in the dependent variable. For a univariate regression, R2 is equal to the correlation between the dependent and independent variable, squared.
For a linear regression equation, Y = α + βX + ε, if we define the total sum of squares, TSS, the explained sum of squares, ESS, and the residual sum of squares, RSS, as follows:
Then R2 can be calculated as follows:
Using our previous definitions and dividing both the denominator and numerator by (n − 1), we can express R2 in terms of the variance of ε and y,
In other words, R2 is equal to one minus the fraction of risk that is idiosyncratic, or equal to the faction of risk that is systematic,